Файл 1.

Задача отыскания приближения к корню уравнения с заданной точностью состоит в поиске числа , удовлетворяющего условию:

Метод бисекции является:

Итерационным методом решения уравнения

Апостериорная оценка погрешности для метода простой итерации имеет вид:

Методом Ньютона решается уравнение: . Расчетная формула имеет вид:

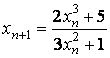
Радиус интервала неопределенности простого корня уравнения можно вычислить по формуле:

Уравнение имеет вид: Что можно сказать о корнях функции:

Первый корень – кратный, второй – простой

Оценка погрешности в методе бисекции имеет вид:

Критерий окончания для метода простой итерации имеет вид:

Расчетная формула метода Ньютона имеет вид:

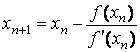
Число обусловленности задачи нахождения простого корня имеет вид:

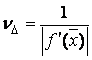
Приближенное значение корня - это такое значение, для которого выполняется условие:

Абсолютная погрешность не превышает

Дано уравнение: . Применяется метод Ньютона с начальным приближением . С какой точностью будет получен корень уравнения после 2-х шагов по методу Ньютона :

0.02

Для достижения точности применяют следующий критерий окончания метода бисекций :

,

Пусть уравнение преобразовано к виду удобному для итерации . Условие сходимости метода простой итерации: в некоторой - окрестности корня должно выполняться условие:

Известен радиус неопределенности простого корня уравнения. С какой точностью можно вычислить корень :

Сколько вещественных корней имеет уравнение :

Один

Первая и вторая производная функции f(x) должны сохранять свой знак для уточнения корня методами:

Ньютона

Файл 2.

 

Какие из приведенных методов относятся  к методам решения нелинейного уравнения:

·        25% Метод Ньютона

·        25% Метод деления пополам  

·        25%  метод простой итерации

·        25% метод хорд

Что из перечисленного НЕ относится к методу простой итерации

·        50% метод хорд

·          50% метод половинного деления

 

 Файл 2.

 

1.      Какие из приведенных методов относятся  к методам решения нелинейного уравнения:

·        33.333% Метод Ньютона

·        33.333% Метод деления пополам

·        33.333% Метод хорд

2.      Что из перечисленного НЕ относится к методу простой итерации

·        50% метод хорд

·        50% метод половинного деления

 

Файл 3.

Установите соответствие

Метод Ньютона является

частным случаем метода простой итерации

Метод Симпсона является

частным случаем метода Ньютона-Котеса

Метод Эйлера является

частным случаем метода Рунге-Кутты

Метод трапеции

является методом расчета определенного интеграла

Файл 5.

Метод Ньютона  - это метод  уточнения  корня.

Метод постой итерации, в котором устанавливается требование равенства нулю для первой производной от величины (lf(x)-x), называется методом Ньютона.